65载数学谜题终迎重大突破!
复旦大学林伟南、王国祯携手加州大学洛杉矶分校徐宙利,成功破解126维空间Kervaire不变量之谜。
三位学者均系北京大学数学科学学院校友,该成果曾作为北大126周年校庆献礼进行学术展示,现已正式发表于预印本平台。

△图片来源:北京大学数学科学学院
这项研究攻克了高维拓扑学领域的关键性猜想,该理论被学界视作"基础性支柱"——若其被颠覆,大量相关推论将面临重构风险!
Kervaire不变量是判定流形能否通过特定拓扑操作转化为标准球面的关键指标。该数值为0表示存在转化可能,为1则意味着存在不可转化的特殊结构。
早在上世纪60年代,数学家已证实2ⁿ−2维度(2、6、14、30)存在此类特殊流形。
即便对数学背景有限的读者,这四个数值呈现的指数规律也显而易见:2=2²−2,6=2³−2,14=2⁴−2,30=2⁵−2。
由此自然引申出62(2⁶−2)、126(2⁷−2)、254(2⁸−2)等维度的猜想,但学界长期停滞于62维证明,后续研究陷入僵局。
直至2009年,254及以上维度被证实不存在此类流形,126维遂成为该领域最后待解的谜题。
研究团队创新性地融合算法验证与理论突破,其系统性工作被同行盛赞为"跨时代的学术壮举"。

从百余种可能到唯一确定性
学界长期致力于探索:在哪些维度空间存在无法通过拓扑操作规整为球面的特殊几何结构。
通俗而言,每个新增维度都意味着空间特性的质变。例如在8维与24维空间中,数学家发现了球体最紧密排列方式,而其他维度则可能存在"褶皱"状的特殊构型。

通过识别这些特殊维度,研究者得以深入解析高维空间的本质规律。在林伟南团队取得突破前,学界已锁定2、6、14、30、62维存在特殊流形,并将可能范围缩小至126维。
追溯研究历程,20世纪50年代John Milnor开创的"拓扑手术"理论为关键转折点。该方法通过精确的切割-重构操作,使复杂流形转化为标准球面成为可能。
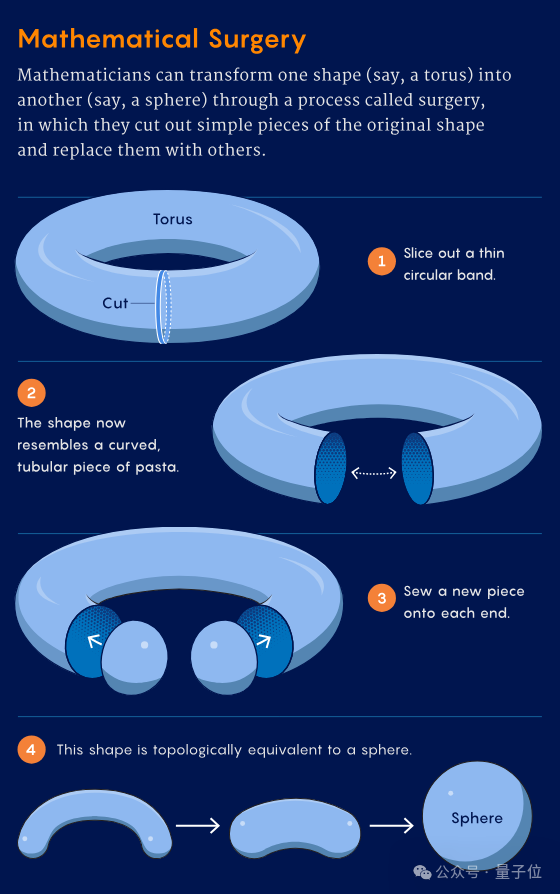
在此框架下,学界发现三类典型情况:某些维度不存在特殊流形;部分维度兼具可转化与不可转化类型;以及存在完全无法转化的特殊维度。
1960年Michel Kervaire提出数值化判定标准后,数学家William Browder于1969年建立重要理论框架,将126维问题的解决指向亚当斯谱序列中的特定计算点。
